Tugas Kuliah: April 2014

Sabtu, 05 April 2014

bab 6 distribusi F

DISTRIBUSI F

Distribusi ini juga mempunyai variabel acak yang kontinu. Fungsi identiatasnya mempunyai persamaan:

Dengan variabel acak F memenuhi batas F > 0, K = bilangan yang tetap harganya bergantung pada v1 dan v2 . sedemikian sehingga luas dibawah kurva sama dengan satu, v1= dk pembilang dan v2= dk penyebut.

Jadi distribusi F ini mempunyai dua buah derajat kebebasan. Grafik distribusi F tidak simetrik dan umumnya sedikit positif seperti juga distribusi lainya, untuk keperluan penghitungan dengan distribusi F, daftar distribusi F telah disediakan seperti dapat ditemukan dalam lampiran , daftar 1. Daftar tersebut berisikan nilai-nilai F untuk peluang 0,01 dan 0,05 dengan derajat kebebasan v1 dan v2. Peluang ini sama dengan luas daerah ujung kanan yang diarsir, sedangkan dk=v1 ada pada baris paling atas dan dk=v2 pada kolom paling kiri.

Untuk tiap pasang dk,v1 dan v2,daftar berisikan harga-harga Fdengan luas kedua ini (0,01 atau 0,05)

Untuk tiap dk= v2, daftar terdiri atas dua baris, yang atas untuk peluang p=0,05 dan yang bawah untuk p=0,01.

Contoh: untuk pasangan derajat kebebasan v1=24 dan v2=8, ditulis juga(v1,v2)=(24,8), maka untuk p=0,05 didapat F =3,12 sedangkan untuk p=0,01 didapat F=5,28(lihat daftar1,lampiran). Ini didapat dengan jalan mencari 24 pada baris atas dan 8 pada kolom kiri. Jika dari 24 turun dan dari 8 ke kanan, maka didapat bilangan bilangat tersebut. Yang atas untuk p=0,05 dan yang bawahnya untuk p=0,01.

Notasi lengkap untuk nilai-nilai F dari daftar distribusi F dengan peluang p dan dk=(v1,v2) adalah Fp(v1,v2)

Demikian untuk contoh kita didapat

F0,05(24,8)=3,12 dan F0,01(24,8)=5,28

Meskipun daftar yang diberikan hanya untuk peluang p=0,01 dan p=0,05, tetapi sebenarnya masih bisa didapat nilai-nilai F dengan peluang 0,99 dan 0,95.

Untuk ini digunakan hubungan

Dalam rumus diatas perhatikan antara p dan (1-p)dan pertukaran antara derajat kebebasan (v1,v2) menjadi (v2,v1)

Contoh: telah didapat F0,05(24,8)=3,12

makaF 0,95(8,24)= 0,321.

bab 6 distribusi T

Distribusi t
1. Dasar
Distribusi probabilitas t-Student diturunkan dari distribusi probabilitas normal baku, dalam bentuk yang berkaitan dengan distribusi probabilitas khi-kuadrat, yakni
dengan z1, z2, z3, . . . sebagai distribusi probabilitas normal baku dan
c2n = z21 + z22 + z23 + . . . + z2n
dari distribusi probabilitas khi-kuadrat
Fungsi Densitas
Fungsi densitas distribusi probabilitas t adalah

dengan n = derajat kebebasan
Distribusi probabilitas t-Student memiliki derajat kebebasan n
Jika n à ∞ maka t à z yakni distribusi probabilitas t mendekati distribusi probabilitas normal baku
Distribusi probabilitas t adalah simetris terhadap rerata (rerata = 0) sehingga memiliki nilai positif dan negatif
Dalam bentuk grafik

3. Rerata dan Variansi
Rerata mt = 0
Variansi

. Fungsi Distribusi
• Fungsi distribusi bawah pada distribusi probabilitas t-Student disusun ke dalam suatu tabel
• Fungsi distribusi bawah ini dapat juga ditemukan di dalam program komputer seperti Minitab
• Fungsi distribusi atas dapat dicari melalui hubungan FDA = 1 – FDB
• Pada fungsi distribusi bawah
Diketahui : f dan n
Ditabelkan : tf

Tabel Fungsi Distribusi Bawah Distribusi Probabilitas t-Student
• Tabel terlampir
• Untuk membaca tabel diperlukan f dan n sehingga dicari t(f)(n)

Distribusi Probabilitas t-Student melalui pendekatan dari zf

Dari Cornish dan Fisher

6. Hubungan a dan f pada Distribusi Probabilitas t-Student

Pendekatan Distribusi Probabilitas t-Student ke Distribusi Probabilitas Normal Baku
• Makin besar derajat kebebasan n, makin dekat distribusi probabilitas t-Student ke distribusi probabilitas normal baku
• Pada n à ∞ maka t à z
• Pada n = ∞, tabel t = tabel z
• Karena itu, apabila n cukup besar maka kita dapat mencari tf pada tabel zf
• Tabel fungsi distribusi t terlampir menyajikan tf untuk n = 1 sampai n = 100
• Jika dikehendaki, pada n > 100, pencarian tf dapat dilakukan pada tabel zf

bab 6 distribusi normal

Distribusi normal merupakan salah satu distribusi probabilitas yang penting dalam analisis statistika. Distribusi ini memiliki parameter berupa mean dan simpangan baku. Distribusi normal dengan mean = 0 dan simpangan baku = 1 disebut dengan distribusi normal standar. Apabila digambarkan dalam grafik, kurva distribusi normal berbentuk seperti genta (bell-shaped) yang simetris. Perhatikan kurva distribusi normal normal standar berikut:

Sumbu X (horizontal) memiliki range (rentang) dari minus takhingga (‒∞) hingga positif takhingga (+∞). Kurva normal memiliki puncak pada X = 0. Perlu diketahui bahwa luas kurva normal adalah satu (sebagaimana konsep probabilitas). Dengan demikian, luas kurva normal pada sisi kiri = 0,5; demikian pula luas kurva normal pada sisi kanan = 0,5.

Dalam analisis statistika, seringkali kita menentukan probabilitas kumulatif yang dilambangkan dengan notasi P (X<x). Sebagai contoh, P (X<1), apabila diilustrasikan dengan grafik adalah luas kurva normal dari minus takhingga hingga X = 1.

Secara matematis, probabilitas distribusi normal standar kumulatif dapat dihitung dengan menggunakan rumus:

Akan tetapi, kita lebih mudah dengan bantuan tabel distribusi normal. Berikut adalah tabel distribusi normal standar, untuk P (X < x), atau dapat diilustrasikan dengan luas kurva normal standar dari X = minus takhingga sampai dengan X = x.

Contoh penggunaan:
Hitung P (X<1,25)

Penyelesaian: Pada tabel, carilah angka 1,2 pada kolom paling kiri. Selanjutnya, carilah angka 0,05 pada baris paling atas. Sel para pertemuan kolom dan baris tersebut adalah 0,8944.
Dengan demikian, P (X<1,25) adalah 0,8944.
Berikut adalah tabel distribusi normal standar kumulatif:

bab 5 momen (kemiringan dan kurtosis)

1. Ukuran Kemiringan (skewness)

    Merupakan derajat atau ukuran dari ketidaksimetrisan (Asimetri) suatu distribusi data. Kemiringan distribusi data terdapat 3 jenis, yaitu :

    Simetris : menunjukkan letak nilai rata-rata hitung,
median, dan modus berhimpit (berkisar disatu
titik)
    Miring ke kanan : mempunyai nilai modus paling
kecil dan rata-rata hitung
paling besar
    Miring ke kiri : mempunyai nilai modus paling
besar dan rata-rata hitung paling kecil

Kemiringan              simetri (normal)            kemiringan                 Negatif                            positif

Untuk mengukur derajat kecondongan suatu distribusi dinyatakan dengan koefisien kecondongan (koefisien skewness).Ada tiga metode yang bisa digunakan untuk menghitung koefisien skewness yaitu :

    Rumus pearson

 = 1/S (X ̅ - Mod)   Atau  = 3/S (X ̅ – Med)

    Rumus Momen

    Data tidak berkelompok

3 = 1/〖nS〗^2 ∑ ( X1 X ̅ )3

    Data Berkelompok

3 = 1/〖nS〗^3 ∑f i( mi - X ̅ )3

Keterangan
3    = derajat kemiringan
x1    = nilai data ke – i
X ̅     = nilai rata-rata hitung
Fi    = frrekuensi nilai ke i
M1    = nilai titik tengah kelas ke-i
S    = Simpangan Baku
N    = Banyaknya data
Jika    3 = 0 distribusi data simetris
    3 < 0 distribusi data miring ke kiri
    3 > 0 distribusi data miring ke kanan

Rumus bowley

Rumus ini menggunakan nilai kuartil :

    3 = (Q_3+ Q_1- 2Q_2)/(Q_3- Q_1 )
Keterangan :
Q1        = kuartil pertama
Q2        = Kuartil Kedua
Q3        = Kuaril Ketiga

Cara menentukan kemiringannya :
    Jika Q3 – Q2 = Q2 – Q1 sehingga Q3 + Q1 -2Q2 = 0 yang mengakiibatkan 3 = 0, sebaliknya jika distribusi miring maka ada dua kemungkinan yaitu Q1 = Q2 atau Q2 = Q3, dalam hal Q1 = Q2 maka 3 = 1 , dan untuk Q2 = Q3 maka 3 = -1

Ukuran kemiringan data merupakan ukuran yang menunjukan apakah penyebaran data terhadap nilai rata-ratanya bersifat simetris atau tidak. Ukuran kemiringan pada dasarnya merupakan ukuran yang menjelaskan besarnya penyimpangan data dari bentuk simetris. Suat distribusi frekuensi yang miring (tidak simetris) akan memiliki nilai mean, median dan modus yang tidak sama besar (X ̅ ≠ Md ≠ Mo) sehinggan distribusi akan memusat pada salah satu sisi yaitu sisi kanan atau sisi kiri. Hal ini yang menyebabkan bentuk kurva akan miring ke kanan atau ke kiri. Jika kurva miring ke arah kanan (ekornya memanjang ke arah kiri) disebut kemiringan positif, dan jika kurva miring ke arah kiri (ekornya memnjang ke arah kanan) disebut kemiringan negatif.

Analisis kasus :
Tabel 2.1
Cara perhitungan koefisien kecondongan dengan metode
Pearson dari data penghasilan keluarga
penghasila keluarga    X    f    U    fU    Fu2
10-22    16    5    -3    -15    225
23-35    29    6    -2    -12    144
36-48    42    13    -1    -13    169
49-61    55    19    0    0    0
62-74    68    11    1    11    121
75-87    81    11    2    22    484
88-100    94    5    3    15    225
Jumlah        70        ∑ fU = 8    ∑ fU2 = 1368

Sebelum menggunakan rumus terlebih dahulu dicari nilai , mean, median, dan standar deviasinya berikut ini:
Mean :
X ̅ = A + ((∑▒〖f.U〗)/n) . i
        X ̅ = 55 + (8/70) . 3
X ̅ = 56,485

Median :
    Med = Tkbmd + ((1/2 n-fkb)/fmd) . i

Med = 48.5 + ((35-24)/19) . 13
Med = 48.5 + 7,526
Med = 56,026

Standar Deviasi :

        S = i √((n∑f.U^2-(∑f.U^2))/(n(n-1)))
            S = 13 √(((70)-(1368)-(〖8)〗^2)/(70(70-1)))
            S = 13 √19,81
            S = 57,86

Setelah kita dapatkan nilai-nilai diatas, kemudian dimasukan ke dalam rumus koefisein skewness :
α = 3/S (X ̅ - Med)

α = 3/57,86 ( 56,485 – 56,026)

α = 0,0238

dari hasil perhitungan menunjukan bahwa koefisien skewness menghasilkan nilai positif, itu berarti distribusi frekuensi mempunyai bentuk kemiringan yang positif yaitu miring ke arah kanan


2. Ukuran Keruncingan (kurtosis)

Merupakan derajat atau ukuran tinggi rendahnya puncak suatu distribusi data terhadap distribusi normalnya data. Jika bentuk kurva runcingberarti nilai data terkonsentrasi terhadap nilai rata-tata atau nilai penyebarannya kecil, sebaliknya jika bentuk kurva nya tumpul berarti nilai data tersebar terhadap nilai rata-rata atau nilai penyebaran besar. Keruncingan distribusi data ini disebut juga kurtosis.
Derajat keruncingan suatu distribusi frekuensi dapat dibedakan menjadi tiga, yaitu:
    Leptokurtis
Distribusi data yang puncaknya relatif tinggi atau bentuk distribusi yang ujungnya sangat runcing
    Mesokurtis
Distribusi data yang puncaknya tidak terlalu runcing atau tidak terlalu tumpul
    Platikurtis
Distribusi data yang puncaknya terlalu rendah atau terlalu mendatar

            Mesokurtis                              leptokurtis                              platikurtis

Derajat keruncingan distribusi data α4 dapat dihitung berdasarkan rumus berikut
    Data tidak berkelompok
α4 = 1/(nS^4 ) ∑ ( Xi - X ̅)4

    Data berkelompok
α4 = 1/(nS^4 ) ∑ fi ( mi - X ̅ )4

Keterangan :
α4    = Derajat keruncingan
Xi    = nilai data ke – i
        = nilai rata-rata hitung
fi    = frekuensi kelas ke – i
mi    = nilai titik tengah ke –i
S    = simpangan baku
n     = banyaknya data

dari penggunaan rumus diatas akan menghasilkan kemungkinan tiga nilai yaitu :
        α4 = 3 distribusi keruncingan data disebut mesokurtis
        α4 > 3 distribusi keruncingan data disebut leptokurtis
        α4 < 3 distribusi keruncingan data disebut platikurtis

Analisis kasus :
Tabel 2.2
Cara perhitungan koofisien keruncingan
Dari data penghasilan keluarga
Penghasilan keluarga    Frekuensi    U    f.U    f.U2    f.U3    f.U4
10-22    5    -3    -15    45    -135    405
23-35    6    -2    -12    24    -48    96
36-48    13    -1    -13    13    -13    13
49-61    19    0    0    0    0    0
62-74    11    1    11    11    11    11
75-87    11    2    22    44    88    176
88-100    5    3    15    45    135    405
jumlah    70         8    182    38    1106

s = i √((n∑fU^2-(∑f.〖U)〗^2)/(n(n-1)))
s = 13 √(((70)(1368)-(〖8)〗^2)/(70(70-1)))

s = 13 √19,81

s = 57,86

Setelah kita dapatkan nilai diatas, kemudian dimasukan ke dalam rumus koefisein kurtosis :

α4 = [(∑f.U^4)/n-4{(∑f.U^3)/n}{(∑f.U^ )/n}+6{(∑f〖.U〗^2)/n} {(∑f.U)/n}^2-3{(∑f.U)/n}^4 ] i^4/s^4

α4 = [1106/70-4{38/70}{8/70}+6{182/70} {8/70}^2-3{8/70}^4 ] 〖13〗^4/〖57.86〗^4

α4 = (15.7557) (0,00255)

α4 = 0.040

Kamis, 03 April 2014

bab 4 ukuran penyimpangan

PENGUKURAN PENYIMPANGAN

Pengukuran penyimpangan adalah suatu ukuran yang menunjukkan tinggi rendahnya perbedaan data yang diperoleh dari rata-ratanya. Ukuran penyimpangan digunakan untuk mengetahui luas penyimpangan data atau homogenitas data. Dua variabel data yang memiliki mean sama belum tentu memiliki kualitas yang sama, tergantung dari besar atau kecil ukuran penyebaran datanya. Ada bebarapa macam ukuran penyebaran data, namun yang umum digunakan adalah standar deviasi.

Macam-macam ukuran penyimpangan data adalah :

Jangkauan (range)
Simpangan rata-rata (mean deviation)
Simpangan baku (standard deviation)
Varians (variance)
Koefisien variasi (Coefficient of variation)

1. Jangkauan (range)

Range adalah salah satu ukuran statistik yang menunjukan jarak penyebaran data antara nilai terendah (Xmin) dengan nilai tertinggi (Xmax). Ukuran ini sudah digunakan pada pembahasan daftar distribusi frekuensi. Adapun rumusnya adalah

Contoh :
Berikut ini nilai ujian semester dari 3 mahasiswa
A = 60 55 70 65 50 80 40
B = 50 55 60 65 70 65 55
C = 60 60 60 60 60 60 60
Dari data diatas dapat diketahui bahwa
A = memiliki Xmax=80, Xmin= 40 , R = 40 , meanya 60
B = memiliki Xmax=70, Xmin= 50 , R = 20 , meanya 60
C = memiliki Xmax=60, Xmin= 60 , R = 0 , meanya 60
Dari contoh di atas dapat disimpulkan bahwa :
a. Semakin kecil rangenya maka semakin homogen distribusinya
b. Semakin besar rangenya maka semakin heterogen distribusinya
c. Semakin kecil rangenya, maka meannya merupakan wakil yang representatif
d. Semakin besar rangenya maka meannya semakin kurang representatif
2. Simpangan Rata-rata (mean deviation)

Simpangan rata-rata merupakan penyimpangan nilai-nilai individu dari nilai rata-ratanya. Rata-rata bisa berupa mean atau median. Untuk data mentah simpangan rata-rata dari median cukup kecil sehingga simpangan ini dianggap paling sesuai untuk data mentah. Namun pada umumnya, simpangan rata-rata yang dihitung dari mean yang sering digunakan untuk nilai simpangan rata-rata.

Data tunggal dengan seluruh skornya berfrekuensi satu

dimana xi merupakan nilai data

Data tunggal sebagian atau seluluh skornya berfrekuensi lebih dari satu

dimana xi merupakan nilai data

Data kelompok ( dalam distribusi frekuensi)

dimana xi merupakan tanda kelas dari interval ke-i dan fi merupakan frekuensi interval ke-i

Contoh :
Dari tabel diperoleh

3. Simpangan Baku (standard deviation)

Standar deviasi merupakan ukuran penyebaran yang paling banyak digunakan. Semua gugus data dipertimbangkan sehingga lebih stabil dibandingkan dengan ukuran lainnya. Namun, apabila dalam gugus data tersebut terdapat nilai ekstrem, standar deviasi menjadi tidak sensitif lagi, sama halnya seperti mean.

Standar Deviasi memiliki beberapa karakteristik khusus lainnya. SD tidak berubah apabila setiap unsur pada gugus datanya di tambahkan atau dikurangkan dengan nilai konstan tertentu. SD berubah apabila setiap unsur pada gugus datanya dikali/dibagi dengan nilai konstan tertentu. Bila dikalikan dengan nilai konstan, standar deviasi yang dihasilkan akan setara dengan hasilkali dari nilai standar deviasi aktual dengan konstan.

Rumus Simpangan Baku untuk Data Tunggal

untuk data sample menggunakan rumus

untuk data populasi menggunkan rumus

Contoh :
Selama 10 kali ulangan semester ini sobat mendapat nilai 91, 79, 86, 80, 75, 100, 87, 93, 90,dan 88. Berapa simpangan baku dari nilai ulangan sobat?

Jawab
Soal di atas menanyakan simpangan baku dari data populasi jadi menggunakan rumus simpangan baku untuk populasi.
Kita cari dulu rata-ratanya
rata-rata = (91+79+86+80+75+100+87+93+90+88)/10 = 869/10 = 85,9

Kita masukkan ke rumus

Rumus Simpangan Baku Untuk Data Kelompok

untuk sample menggunakan rumus

untuk populasi menggunakan rumus

Contoh :
Diketahui data tinggi badan 50 siswa samapta kelas c adalah sebagai berikut

hitunglah berapa simpangan bakunya
1. Kita cari dulu rata-rata data kelompok tersebut

2. Setelah ketemu rata-rata dari data kelompok tersebut kita bikin tabel untuk memasukkannya ke rumus simpangan baku

4. Varians (variance)

Varians adalah salah satu ukuran dispersi atau ukuran variasi. Varians dapat menggambarkan bagaimana berpencarnya suatu data kuantitatif. Varians diberi simbol σ² (baca: sigma kuadrat) untuk populasi dan untuk s²sampel.

Selanjutnya kita akan menggunakan simbol s² untuk varians karena umumnya kita hampir selalu berkutat dengan sampel dan jarang sekali berkecimpung dengan populasi.

Rumus varian atau ragam data tunggal untuk populasi

Rumus varian atau ragam data tunggal untuk sampel

Rumus varian atau ragam data kelompok untuk populasi

Rumus varian atau ragam data kelompok untuk sampel

Keterangan:
σ² = varians atau ragam untuk populasi
S² = varians atau ragam untuk sampel
f_i = Frekuensi
x_i = Titik tengah
x¯ = Rata-rata (mean) sampel dan μ = rata-rata populasi
n = Jumlah data

5. Koefisien variasi (Coefficient of variation)

Koefisien variasi merupakan suatu ukuran variansi yang dapat digunakan untuk membandingkan suatu distribusi data yang mempunyai satuan yang berbeda. Kalau kita membandingkan berbagai variansi atau dua variabel yang mempunyai satuan yang berbeda maka tidak dapat dilakukan dengan menghitung ukuran penyebaran yang sifatnya absolut.

Koefisien variasi adalah suatu perbandingan antara simpangan baku dengan nilai rata-rata dan dinyatakan dengan persentase.

Besarnya koefisien variasi akan berpengaruh terhadap kualitas sebaran data. Jadi jika koefisien variasi semakin kecil maka datanya semakin homogen dan jika koefisien korelasi semakin besar maka datanya semakin heterogen.

Daftas Pustaka :

Suharyadi, & Purwanto. (2009). In Statistika untuk Ekonomi dan Keuangan Modern. Jakarta: Salemba Empat.

Sudjana. (1991). In Statistika. Bandung: Tarsito.
http://www.smartstat.info/statistika/statisika-deskriptif/ukuran-penyebaran-measures-of-dispersion.html
http://rumushitung.com/2013/04/05/rumus-simpangan-baku/
http://digensia.wordpress.com/2012/03/15/statistik-deskriptif/
http://okemath.com/?page_id=394

Daftas Pustaka :

Suharyadi, & Purwanto. (2009). In Statistika untuk Ekonomi dan Keuangan Modern. Jakarta: Salemba Empat.

bab 3 ukuran pemusatan

Salah satu aspek yang paling penting untuk menggambarkan distribusi data adalah nilai pusat data pengamatan (Central Tendency). Setiap pengukuran aritmatika yang ditujukan untuk menggambarkan suatu nilai yang mewakili nilai pusat atau nilai sentral dari suatu gugus data (himpunan pengamatan) dikenal sebagai ukuran pemusatan data (tendensi sentral). Terdapat tiga ukuran pemusatan data yang sering digunakan, yaitu:

Mean (Rata-rata hitung/rata-rata aritmetika)
Median
Mode

Pada artikel ini akan di bahas mengenai pengertian beberapa ukuran pemusatan data yang dilengkapi dengan contoh perhitungan, baik untuk data tunggal ataupun data yang sudah dikelompokkan dalam tabel distribusi frekuensi. Selain ukuran statistik di atas, akan dibahas juga mengenai beberapa ukuran statistik lainnya, seperti Rata-rata Ukur (Geometric Mean), Rata-rata Harmonik (H) serta beberapa karakteristik penting yang perlu dipahami untuk ukuran tendensi sentral yang baik serta bagaimana memilih atau menggunakan nilai tendensi sentral yang tepat.

(1) Mean (arithmetic mean)

Rata-rata hitung atau arithmetic mean atau sering disebut dengan istilah mean saja merupakan metode yang paling banyak digunakan untuk menggambarkan ukuran tendensi sentral. Mean dihitung dengan menjumlahkan semua nilai data pengamatan kemudian dibagi dengan banyaknya data. Definisi tersebut dapat di nyatakan dengan persamaan berikut:
Sampel: $\overline{x}=\dfrac{x_1+x_2+x_3+\dots +x_n}{n}\ {\rm atau}\ \overline{x}=\dfrac{\sum^n_{i=1}{x_i}}{n}\ {\rm atau}\ \overline{x}=\dfrac{\Sigma x}{n}$ Populasi: $\mu =\dfrac{x_1+x_2+x_3+\dots +x_n}{n}\ {\rm atau}\ \mu =\dfrac{\sum^n_{i=1}{x_i}}{n}\ {\rm atau}\ \mu =\dfrac{\Sigma x}{n}$ Keterangan:∑ = lambang penjumlahan semua gugus data pengamatan n = banyaknya sampel data N = banyaknya data populasi $\bar x$ = nilai rata-rata sampel μ = nilai rata-rata populasi Mean dilambangkan dengan $\bar x$ (dibaca "x-bar") jika kumpulan data ini merupakan contoh (sampel) dari populasi, sedangkan jika semua data berasal dari populasi, mean dilambangkan dengan μ (huruf kecil Yunani mu).

Sampel statistik biasanya dilambangkan dengan huruf Inggris, $\bar x$ , sementara parameter-parameter populasi biasanya dilambangkan dengan huruf Yunani, misalnya μ

a. Rata-rata hitung (Mean) untuk data tunggal

Contoh 1:
Hitunglah nilai rata-rata dari nilai ujian matematika kelas 3 SMU berikut ini: 2; 4; 5; 6; 6; 7; 7; 7; 8; 9
Jawab:
$\overline{x}=\dfrac{\Sigma x}{n}=\dfrac{{2\ +4\ +5\ +6\ +6\ +7\ +7\ +7\ +8\ +9}}{10}=\dfrac{{61}}{10}=6.10$
Nilai rata-rata dari data yang sudah dikelompokkan bisa dihitung dengan menggunakan formula berikut:
$\bar x=\dfrac{f_1x_1+f_2x_2+\dots .+f_nx_n}{f_1+f_2+\dots +f_n}=\dfrac{{\Sigma f}_ix_i}{\Sigma f_i}$
Keterangan: ∑ = lambang penjumlahan semua gugus data pengamatan f_i = frekuensi data ke-i n = banyaknya sampel data $\bar x$ = nilai rata-rata sampel
Contoh 2:
Berapa rata-rata hitung pada tabel frekuensi berikut:

x_i	f_i
70	5
69	6
45	3
80	1
56	1

Catatan: Tabel frekuensi pada tabel di atas merupakan tabel frekuensi untuk data tunggal, bukan tabel frekuensi dari data yang sudah dikelompokkan berdasarkan selang/kelas tertentu.
Jawab:

x_i	f_i	f_ix_i
70	5	350
69	6	414
45	3	135
80	1	80
56	1	56
Jumlah	16	1035

$\overline{x}=\dfrac{{\Sigma f}_ix_i}{\Sigma f_i}$
$\overline{x}=\dfrac{1035}{{\rm 16}}=64.6$

b. Mean dari data distribusi Frekuensi atau dari gabungan:

Distribusi Frekuensi: Rata-rata hitung dari data yang sudah disusun dalam bentuk tabel distribusi frekuensi dapat ditentukan dengan menggunakan formula yang sama dengan formula untuk menghitung nilai rata-rata dari data yang sudah dikelompokkan, yaitu: $\bar x=\dfrac{{\Sigma f}_ix_i}{\Sigma f_i}$
Keterangan:
∑ = lambang penjumlahan semua gugus data pengamatan f_i = frekuensi data ke-i $\bar x$ = nilai rata-rata sampel
Contoh 3:
Tabel berikut ini adalah nilai ujian statistik 80 mahasiswa yang sudah disusun dalam tabel frekuensi. Berbeda dengan contoh 2, pada contoh ke-3 ini, tabel distribusi frekuensi dibuat dari data yang sudah dikelompokkan berdasarkan selang/kelas tertentu (banyak kelas = 7 dan panjang kelas = 10).

Kelas ke-	Nilai Ujian	f_i
1	31 - 40	2
2	41 - 50	3
3	51 - 60	5
4	61 - 70	13
5	71 - 80	24
6	81 - 90	21
7	91 - 100	12
	Jumlah	80

Jawab:
Buat daftar tabel berikut, tentukan nilai pewakilnya (x_i) dan hitung f_ix_i.

Kelas ke-	Nilai Ujian	f_i	x_i	f_ix_i
1	31 - 40	2	35.5	71.0
2	41 - 50	3	45.5	136.5
3	51 - 60	5	55.5	277.5
4	61 - 70	13	65.5	851.5
5	71 - 80	24	75.5	1812.0
6	81 - 90	21	85.5	1795.5
7	91 - 100	12	95.5	1146.0
	Jumlah	80		6090.0

$\overline{x}=\dfrac{{\Sigma f}_ix_i}{\Sigma f_i}$
$\bar {x}=\dfrac{6090}{{\rm 80}}=76.1$
Catatan: Pendekatan perhitungan nilai rata-rata hitung dengan menggunakan distribusi frekuensi kurang akurat dibandingkan dengan cara perhitungan rata-rata hitung dengan menggunakan data aktualnya. Pendekatan ini seharusnya hanya digunakan apabila tidak memungkinkan untuk menghitung nilai rata-rata hitung dari sumber data aslinya.

**Rata-rata Gabungan atau rata-rata terboboti (Weighted Mean)**

Rata-rata gabungan (disebut juga grand mean, pooled mean, atau rata-rata umum) adalah cara yang tepat untuk menggabungkan rata-rata hitung dari beberapa sampel.
$\overline{x}=\dfrac{{\Sigma n}_ix_i}{\Sigma n_i}=\overline{x}=\dfrac{{\Sigma f}_ix_i}{\Sigma f_i}$
Contoh 4:
Tiga sub sampel masing-masing berukuran 10, 6, 8 dan rata-ratanya 145, 118, dan 162. Berapa rata-ratanya?
Jawab:
$\overline{x}=\dfrac{{\Sigma n}_ix_i}{\Sigma n_i}=\dfrac{\left({\rm 10}\right)\left({\rm 145}\right){\rm +}\left({\rm 6}\right)\left({\rm 118}\right){\rm +}\left({\rm 8}\right){\rm (162)}}{{\rm 10+6+8}}=143.9$

(2) Median

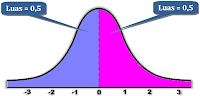
Median dari n pengukuran atau pengamatan x₁, x₂ ,..., x_n adalah nilai pengamatan yang terletak di tengah gugus data setelah data tersebut diurutkan. Apabila banyaknya pengamatan (n) ganjil, median terletak tepat ditengah gugus data, sedangkan bila n genap, median diperoleh dengan cara interpolasi yaitu rata-rata dari dua data yang berada di tengah gugus data. Dengan demikian, median membagi himpunan pengamatan menjadi dua bagian yang sama besar, 50% dari pengamatan terletak di bawah median dan 50% lagi terletak di atas median. Median sering dilambangkan dengan $\tilde{x}$ (dibaca "x-tilde") apabila sumber datanya berasal dari sampel $\tilde{\mu}$ (dibaca "μ-tilde") untuk median populasi. Median tidak dipengaruhi oleh nilai-nilai aktual dari pengamatan melainkan pada posisi mereka. Prosedur untuk menentukan nilai median, pertama urutkan data terlebih dahulu, kemudian ikuti salah satu prosedur berikut ini:

Banyak data ganjil → mediannya adalah nilai yang berada tepat di tengah gugus data
Banyak data genap → mediannya adalah rata-rata dari dua nilai data yang berada di tengah gugus data

a. Median data tunggal:

Untuk menentukan median dari data tunggal, terlebih dulu kita harus mengetahui letak/posisi median tersebut. Posisi median dapat ditentukan dengan menggunakan formula berikut:
$Posisi Median=\dfrac{(n+1)}{2}$

dimana n = banyaknya data pengamatan.
Median apabila n ganjil:
Contoh 5:
Hitunglah median dari nilai ujian matematika kelas 3 SMU berikut ini: 8; 4; 5; 6; 7; 6; 7; 7; 2; 9; 10
Jawab:

data: 8; 4; 5; 6; 7; 6; 7; 7; 2; 9; 10
setelah diurutkan: 2; 4; 5; 6; 6; 7; 7; 7; 8; 9; 10
banyaknya data (n) = 11
posisi Me = ½(11+1) = 6
jadi Median = 7 (data yang terletak pada urutan ke-6)

Nilai Ujian	2	4	5	6	6	7	7	7	8	9	10
Urutan data ke-	1	2	3	4	5	6	7	8	9	10	11
						↑

Median apabila n genap:
Contoh 6:
Hitunglah median dari nilai ujian matematika kelas 3 SMU berikut ini: 8; 4; 5; 6; 7; 6; 7; 7; 2; 9
Jawab:

data: 8; 4; 5; 6; 7; 6; 7; 7; 2; 9
setelah diurutkan: 2; 4; 5; 6; 6; 7; 7; 7; 8; 9
banyaknya data (n) = 10
posisi Me = ½(10+1) = 5.5
Data tengahnya: 6 dan 7
jadi Median = ½ (6+7) = 6.5 (rata-rata dari 2 data yang terletak pada urutan ke-5 dan ke-6)

Nilai Ujian	2	4	5	6	6		7	7	7	8	9
Urutan data ke-	1	2	3	4	5		6	7	8	9	10
						↑

b. Median dalam distribusi frekuensi:

Formula untuk menentukan median dari tabel distribusi frekuensi adalah sebagai berikut:
$Me{\rm{ = b + p}}\left( {\dfrac{{\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{n - F}}}}{{\rm{f}}}} \right)$

b = batas bawah kelas median dari kelas selang yang mengandung unsur atau memuat nilai median

p = panjang kelas median

n = ukuran sampel/banyak data

f = frekuensi kelas median

F = Jumlah semua frekuensi dengan tanda kelas lebih kecil dari kelas median (∑f_i)

Contoh 7:
Tentukan nilai median dari tabel distribusi frekuensi pada Contoh 3 di atas!
Jawab:

Kelas ke-	Nilai Ujian	f_i	f_kum
1	31 - 40	2	2
2	41 - 50	3	5
3	51 - 60	5	10
4	61 - 70	13	23
5	71 - 80	24	47	←letak kelas median
6	81 - 90	21	68
7	91 - 100	12	80
8	Jumlah	80

Letak kelas median: Setengah dari seluruh data = 40, terletak pada kelas ke-5 (nilai ujian 71-80)
b = 70.5, p = 10
n = 80, f = 24
f = 24 (frekuensi kelas median)
F = 2 + 3 + 5 + 13 = 23

$Me{\rm{ = b + p}}\left( {\dfrac{{\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{n - F}}}}{{\rm{f}}}} \right){\rm{ = 70}}.{\rm{5 + 10}}\left( {\dfrac{{\dfrac{{\rm{1}}}{{\rm{2}}}\left( {{\rm{80}}} \right){\rm{ - 23}}}}{{{\rm{24}}}}} \right){\rm{ = 77}}.{\rm{58}}$

(3) Mode

Mode adalah data yang paling sering muncul/terjadi. Untuk menentukan modus, pertama susun data dalam urutan meningkat atau sebaliknya, kemudian hitung frekuensinya. Nilai yang frekuensinya paling besar (sering muncul) adalah modus. Modus digunakan baik untuk tipe data numerik atau pun data kategoris. Modus tidak dipengaruhi oleh nilai ekstrem. Beberapa kemungkinan tentang modus suatu gugus data:

Apabila pada sekumpulan data terdapat dua mode, maka gugus data tersebut dikatakan bimodal.
Apabila pada sekumpulan data terdapat lebih dari dua mode, maka gugus data tersebut dikatakan multimodal.
Apabila pada sekumpulan data tidak terdapat mode, maka gugus data tersebut dikatakan tidak mempunyai modus.

Meskipun suatu gugus data mungkin saja tidak memiliki modus, namun pada suatu distribusi data kontinyu, modus dapat ditentukan secara analitis.

Untuk gugus data yang distribusinya simetris, nilai mean, median dan modus semuanya sama.
Untuk distribusi miring ke kiri (negatively skewed): mean < median < modus
untuk distribusi miring ke kanan (positively skewed): terjadi hal yang sebaliknya, yaitu mean > median > modus.

Hubungan antara ketiga ukuran tendensi sentral untuk data yang tidak berdistribusi normal, namun hampir simetris dapat didekati dengan menggunakan rumus empiris berikut:

Mean - Mode = 3 (Mean - Median)

a. Modus Data Tunggal:

Contoh 8:
Berapa modus dari nilai ujian matematika kelas 3 SMU berikut ini:

2, 4, 5, 6, 6, 7, 7, 7, 8, 9
2, 4, 6, 6, 6, 7, 7, 7, 8, 9
2, 4, 6, 6, 6, 7, 8, 8, 8, 9
2, 4, 5, 5, 6, 7, 7, 8, 8, 9
1, 2, 3, 4, 5, 6, 7, 8, 9, 10

Jawab:

2, 4, 5, 6, 6, 7, 7, 7, 8, 9→ Nilai yang sering muncul adalah angka 7 (frekuensi terbanyak = 3), sehingga Modus (M) = 7
2, 4, 6, 6, 6, 7, 7, 7, 8, 9 → Nilai yang sering muncul adalah angka 6 dan 7 (masing-masing muncul 3 kali), sehingga Modusnya ada dua, yaitu 6 dan 7. Gugus data tersebut dikatakan bimodal karena mempunyai dua modus. Karena ke-2 mode tersebut nilainya berurutan, mode sering dihitung dengan menghitung nilai rata-rata keduanya, ½ (6+7) = 6.5.
2, 4, 6, 6, 6, 7, 8, 8, 8, 9 → Nilai yang sering muncul adalah angka 6 dan 8 (masing-masing muncul 3 kali), sehingga Modusnya ada dua, yaitu 6 dan 8. Gugus data tersebut dikatakan bimodal karena mempunyai dua modus. Nilai mode tunggal tidak dapat dihitung karena ke-2 mode tersebut tidak berurutan.
2, 4, 5, 5, 6, 7, 7, 8, 8, 9 → Nilai yang sering muncul adalah angka 5, 6 dan 7 (masing-masing muncul 2 kali), sehingga Modusnya ada tiga, yaitu 5, 6 dan 7. Gugus data tersebut dikatakan multimodal karena modusnya lebih dari dua.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10 → Pada gugus data tersebut, semua frekuensi data sama, masing-masing muncul satu kali, sehingga gugus data tersebut dikatakan tidak mempunyai modusnya

b. Mode dalam Distribusi Frekuensi:

$Mo{\rm =b+p}\left(\dfrac{{{\rm b}}_{{\rm 1}}}{{{\rm b}}_{{\rm 1}}{\rm +}{{\rm b}}_{{\rm 2}}}\right)$
dimana:

Mo = modal = kelas yang memuat modus

b = batas bawah kelas modal

p = panjang kelas modal

b_mo = frekuensi dari kelas yang memuat modus (yang nilainya tertinggi)

b1= b_mo – b_mo-1 = frekuensi kelas modal – frekuensi kelas sebelumnya

b2 = b_mo – b_mo+1 = frekuensi kelas modal – frekuensi kelas sesudahnya

Contoh 9:
Tentukan nilai median dari tabel distribusi frekuensi pada Contoh 3 di atas!
Jawab:

Kelas ke-	Nilai Ujian	f_i
1	31 - 40	2
2	41 - 50	3
3	51 - 60	5
4	61 - 70	13
			→ b1 = (24 – 13) = 11
5	71 - 80	24	← kelas modal (frekuensinya paling besar)
			→ b2 =(24 – 21) =3
6	81 - 90	21
7	91 - 100	12
8	Jumlah	80

Kelas modul =kelas ke-5
b = 71-0.5 = 70.5
b1 = 24 -13 = 11
b2 = 24 – 21 = 3
p = 10

$Mo{\rm =b+p}\left(\dfrac{{{\rm b}}_{{\rm 1}}}{{{\rm b}}_{{\rm 1}}{\rm +}{{\rm b}}_{{\rm 2}}}\right){\rm =70.5+10}\left(\dfrac{{\rm 11}}{{\rm 11+3}}\right){\rm =78.36}$
Selain tiga ukuran tendensi sentral di atas (mean, median, dan mode), terdapat ukuran tendensi sentral lainnya, yaitu rata-rata ukur (Geometric Mean) dan rata-rata harmonis (Harmonic Mean)

(4) Rata-rata Ukur (Geometric Mean)

Untuk gugus data positif x₁, x₂, …, x_n, rata-rata geometrik adalah akar ke-n dari hasil perkalian unsur-unsur datanya. Secara matematis dapat dinyatakan dengan formula berikut:
$U = \sqrt[n]{{{x_1}.{x_2}.{x_3} \ldots .{x_n}}}\;{\rm{atau}}\;U = \sqrt[n]{{\prod\limits_{i = 1}^n {{x_i}} }}\;{\rm{atau}}\;{\rm{Log}}(U) = \dfrac{{\Sigma \log ({x_i})\;}}{n}$
Dimana: U = rata-rata ukur (rata-rata geometrik) n = banyaknya sampel Π = Huruf kapital π (pi) yang menyatakan jumlah dari hasil kali unsur-unsur data. Rata-rata geometrik sering digunakan dalam bisnis dan ekonomi untuk menghitung rata-rata tingkat perubahan, rata-rata tingkat pertumbuhan, atau rasio rata-rata untuk data berurutan tetap atau hampir tetap atau untuk rata-rata kenaikan dalam bentuk persentase.

a. Rata-rata ukur untuk data tunggal

Contoh 10:
Berapakah rata-rata ukur dari data 2, 4, 8?
Jawab:
$U=\sqrt[3]{\left(2\right)\left(4\right)(8)}=\sqrt[3]{64}=4$
atau:
$Log(U) = \dfrac{{\Sigma \log ({x_i})\;}}{n}$
$Log\left( U \right) = \dfrac{{\log \left( 2 \right)\; + \log \left( 4 \right)\; + \log \left( 8 \right)\;}}{3} = \dfrac{{0.3010 + 0.6021 + 0.9031}}{3} = 0.6021$
$U = {10^{0.6021}} = 4$

b. Distribusi Frekuensi:

$Log\left( U \right) = \dfrac{{\Sigma ({f_i}.\log \left( {{x_i})} \right)\;}}{{\Sigma {f_i}}}$

xi = tanda kelas (nilai tengah)

fi = frekuensi yang sesuai dengan xi

Contoh 11:
Tentukan rata-rata ukur dari tabel distribusi frekuensi pada Contoh 3 di atas!
Jawab

Kelas ke-	Nilai Ujian	fi	xi	log xi	fi.log xi
1	31 - 40	2	35.5	1.5502	3.1005
2	41 - 50	3	45.5	1.6580	4.9740
3	51 - 60	5	55.5	1.7443	8.7215
4	61 - 70	13	65.5	1.8162	23.6111
5	71 - 80	24	75.5	1.8779	45.0707
6	81 - 90	21	85.5	1.9320	40.5713
7	91 - 100	12	95.5	1.9800	23.7600
8	Jumlah	80			149.8091

$\rm Log\left(U\right)=\dfrac{\Sigma {{{\rm f}}_{{\rm i}}{\rm .log} \left(x_i\right)\ }}{\Sigma {{\rm f}}_{{\rm i}}}=\dfrac{149.8091}{80}=1.8726{\rm : U}={10}^{1.8726}=74.5786$

(5) Rata-rata Harmonik (H)

Rata-rata harmonik dari suatu kumpulan data x₁, x₂, …, x_n adalah kebalikan dari nilai rata-rata hitung (aritmetik mean). Secara matematis dapat dinyatakan dengan formula berikut:
$H=\dfrac{n}{\sum{\left(\dfrac{1}{x_i}\right)}}$
Secara umum, rata-rata harmonic jarang digunakan. Rata-rata ini hanya digunakan untuk data yang bersifat khusus. Misalnya,rata-rata harmonik sering digunakan sebagai ukuran tendensi sentral untuk kumpulan data yang menunjukkan adanya laju perubahan, seperti kecepatan.

a. Rata-rata harmonic untuk data tunggal

Contoh 12:
Si A bepergian pulang pergi. Waktu pergi ia mengendarai kendaraan dengan kecepatan 10 km/jam, sedangkan waktu kembalinya 20 km/jam. Berapakah rata-rata kecepatan pulang pergi?
Jawab:
Apabila kita menghitungnya dengan menggunakan rumus jarak dan kecepatan, tentu hasilnya 13.5 km/jam! Apabila kita gunakan perhitungan rata-rata hitung, hasilnya tidak tepat!
$\overline{x}=\dfrac{(10+20)}{2}=15\ {\rm km/jam}$
Pada kasus ini, lebih tepat menggunakan rata-rata harmonik:
$\overline{x}=\dfrac{2}{\dfrac{1}{10}+\dfrac{1}{20}}=\dfrac{40}{3}=13.5\ {\rm km/jam}$

b. Rata-rata Harmonik untuk Distribusi Frekuensi:

$H=\dfrac{\sum f_i}{\sum{\left(\dfrac{f_i}{x_i}\right)}}$
Contoh 13:
Berapa rata-rata Harmonik dari tabel distribusi frekuensi pada Contoh 3 di atas!
Jawab:

Kelas ke-	Nilai Ujian	fi	xi	fi/xi
1	31 - 40	2	35.5	0.0563
2	41 - 50	3	45.5	0.0659
3	51 - 60	5	55.5	0.0901
4	61 - 70	13	65.5	0.1985
5	71 - 80	24	75.5	0.3179
6	81 - 90	21	85.5	0.2456
7	91 - 100	12	95.5	0.1257
8	Jumlah	80		1.1000

$H=\dfrac{\sum f_i}{\sum{\left(\dfrac{f_i}{x_i}\right)}}=\dfrac{80}{1.10000}=72.7283$

Perbandingan Ketiga Rata-rata (Mean):

$\overline{x}=76.10;;U=74.58;;H=72.73$
$H\le U\le \overline{x}=76.10$

Karakteristik penting untuk ukuran tendensi sentral yang baik

Ukuran nilai pusat/tendensi sentral (average) merupakan nilai pewakil dari suatu distribusi data, sehingga harus memiliki sifat-sifat berikut:

Harus mempertimbangkan semua gugus data
Tidak boleh terpengaruh oleh nilai-nilai ekstrim.
Harus stabil dari sampel ke sampel.
Harus mampu digunakan untuk analisis statistik lebih lanjut.

Dari beberapa ukuran nilai pusat, Mean hampir memenuhi semua persyaratan tersebut, kecuali syarat pada point kedua, rata-rata dipengaruhi oleh nilai ekstrem. Sebagai contoh, jika item adalah 2; 4; 5; 6; 6; 6; 7; 7; 8; 9 maka mean, median dan modus semua bernilai sama, yaitu 6. Jika nilai terakhir adalah 90 bukan 9, rata-rata akan menjadi 14.10, sedangkan median dan modus tidak berubah. Meskipun dalam hal ini median dan modus lebih baik, namun tidak memenuhi persyaratan lainnya. Oleh karena itu Mean merupakan ukuran nilai pusat yang terbaik dan sering digunakan dalam analisis statistik.

Kapan kita menggunakan nilai tendensi sentral yang berbeda?

Nilai ukuran pusat yang tepat untuk digunakan tergantung pada sifat data, sifat distribusi frekuensi dan tujuan. Jika data bersifat kualitatif, hanya modus yang dapat digunakan. Sebagai contoh, apabila kita tertarik untuk mengetahui jenis tanah yang khas di suatu lokasi, atau pola tanam di suatu daerah, kita hanya dapat menggunakan modus. Di sisi lain, jika data bersifat kuantitatif, kita dapat menggunakan salah satu dari ukuran nilai pusat tersebut, mean atau median atau modus. Meskipun pada jenis data kuantitatif kita dapat menggunakan ketiga ukuran tendensi sentral, namun kita harus mempertimbangkan sifat distribusi frekuensi dari gugus data tersebut.

Bila distribusi frekuensi data tidak normal (tidak simetris), median atau modus merupakan ukuran pusat yang tepat.
Apabila terdapat nilai-nilai ekstrim, baik kecil atau besar, lebih tepat menggunakan median atau modus.
Apabila distribusi data normal (simetris), semua ukuran nilai pusat, baik mean, median, atau modus dapat digunakan. Namun, mean lebih sering digunakan dibanding yang lainnya karena lebih memenuhi persyaratan untuk ukuran pusat yang baik.
Ketika kita berhadapan dengan laju, kecepatan dan harga lebih tepat menggunakan rata-rata harmonik.
Jika kita tertarik pada perubahan relatif, seperti dalam kasus pertumbuhan bakteri, pembelahan sel dan sebagainya, rata-rata geometrik adalah rata-rata yang paling tepat.